好，今天就不写代码了，来回答一下这个问题，入坑时间还不长，但这个问题也是接触了一段时间了，对于CFD谈不上专业，除了写数值算法和代码以外，对于具体的理论和概念领域了解就少了，所以只能粗浅地谈一下。

首先， 我先来说一下涡旋是如何由于边界的存在而产生的， 先纠正一下题主的一个错误， 在纯粹的无粘流中，涡旋是不可能凭空产生或消失的(谢一楼勘误！)，如以下视频所示，纯粹的无粘流里，粒子会光滑地划过障碍物，在障碍边界上没有“阻力（粘性）”的存在，是不可能产生涡旋的。

那么，在边界存在的时候， 粘性这个东西，到底对于涡旋的产生，起到了什么作用呢？

首先要提一下边界层，边界层是一个较抽象的概念，它大概是说，在这个边界层内部， 主要是粘性主导了流场，而在这个边界层以外，则是欧拉方程主导了流场。

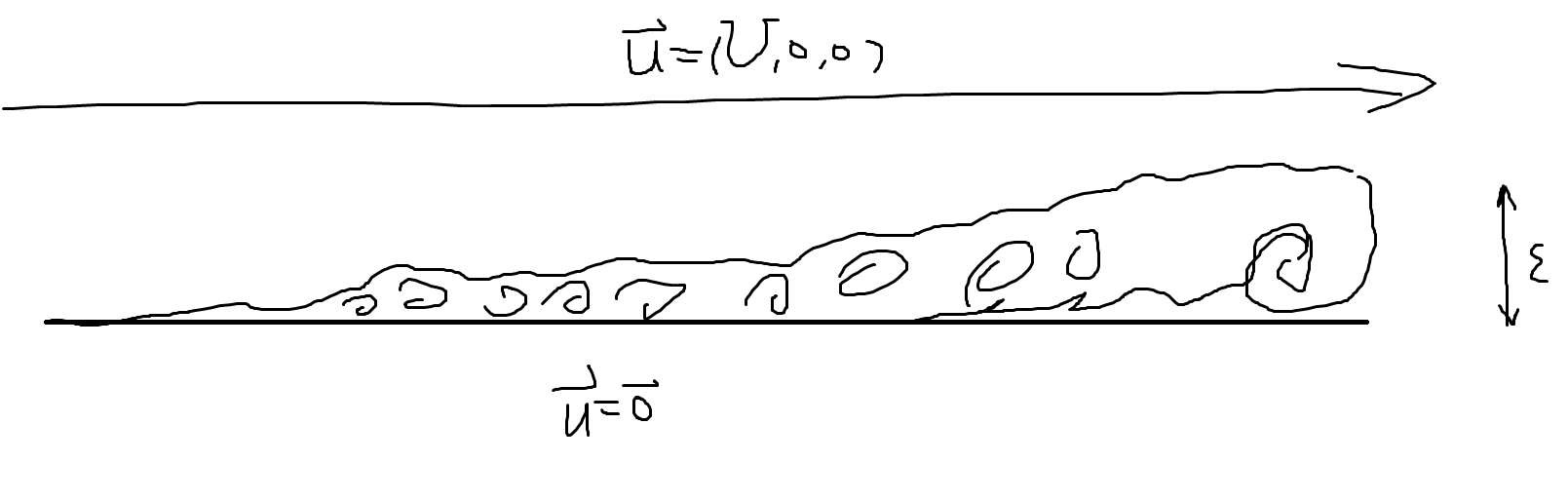
这个边界层到底有多厚呢？？？？下图， 是的，它就只有那么点儿几乎可以忽略的厚度，注意从泛蓝色的那部分起，我认为已经开始分离了？？，所以那厚度不能算进去

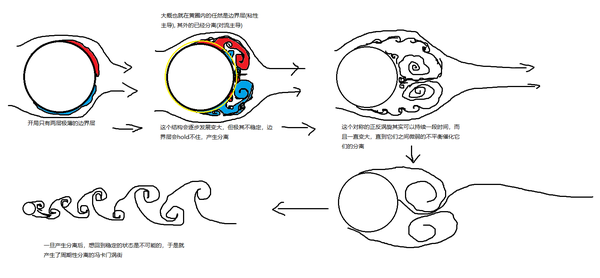
我们现在拿个小球来说一下这东西是怎么产生涡旋， 以及如何影响之后的流场变化的：

实拍到的一些冯卡门涡街：

说到此为止，我讲一讲当时自己在做这一块时接触过的一些理论，

• 我觉得很有趣的是一个 vortex sheet boundary layer模型， 这种模型认为， 这个极薄的边界层，可以通过一个极薄的vortex sheet来表示， 这类模型在按照 旋度方程+potential flow建模的边界层运动完vortex particle后， 再额外地求解一个vortex sheet边界层， 使得这个边界层引入的流场，刚好能够消去切面方向的速度差， 然后再把这个vortex sheet的强度按照一个neumann边界的热扩散模式扩散到周围的vortex particle去， 求解vortex sheet的时候用BEM用Boundary element method来解一个积分方程。
• 这个方法的优点是很优美， 缺点是….遇到复杂一些的边界, 那个积分方程的解算就很难了.
• 第二类型的方法, 没啥说的, 暴力算, 把格子分到无穷小, 求解N-S方程即可, 处理好粘性项
• 这类方法的一个变种是半暴力算, 即通过某种wall-boundary-layer模型(比如解一个局部的stokes方程)来减少边界附近的网格数量, 但所需的网格量基本还是DNS级别的…..而且需要对边界层的厚度和形状有一定预知, 基本不能算个实用的方案.
• 还有一个变种是真.暴力算, 即墙面处的turbulent 模型, 是通过分子模拟空气和墙面的微结构之间的交互而总结出来的(这个尺度NS方程已经不作数), 然后拿这个模型再去建模墙面那一层网格的速度交互, 解stokes方程什么的弱爆了

• 第三类方法, 是混合N-S方程求解以及vortex particle方法的, 这一类是我最喜欢的方法, 目前来来, 在细网格上暴力解算N-S方程, 并且指望它来自动的发展出边界层和旋涡的产生过程, 是鲁棒性最强的做法, 然而一旦远离了边界, 其实是没必要解N-S方程的……在低粘性流体中, 有什么是vortex method做不来的????

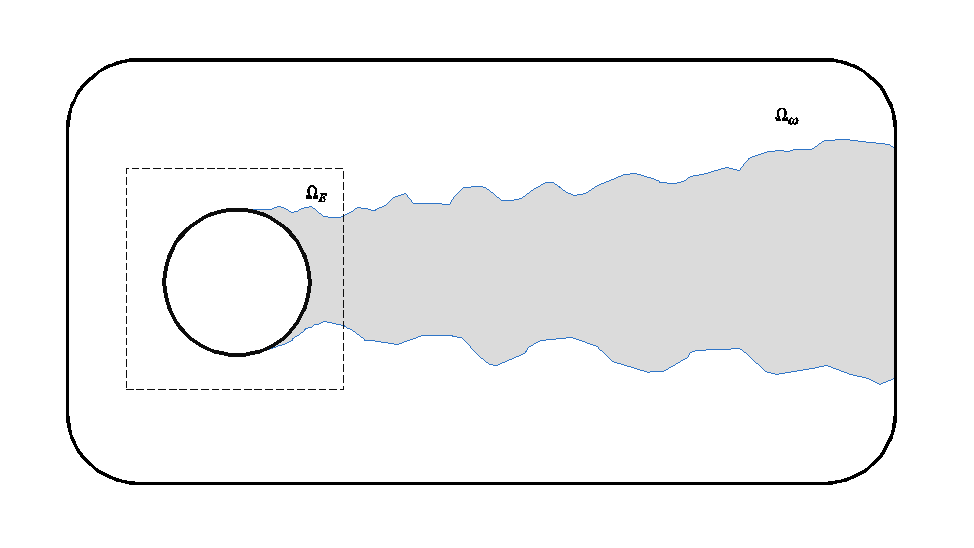
就聊这么多吧, 算是抛砖引个玉

来源：知乎 www.zhihu.com

作者：张心欣

【知乎日报】千万用户的选择，做朋友圈里的新鲜事分享大牛。
点击下载

此问题还有 2 个回答，查看全部。